Teoria matemática Graceli dos caminhos fracionários.

 Onde o fundamental não é o resultado final, mas os caminhos num labirinto de possibilidades fracionárias. E frações  descontínuas por frações de raiz e de logaritmo.

Teoria Graceli dos caminhos.

Onde temos logx/x[n] até parcela y, onde começa a soma com logk/ k [n]   até a parcela fracionaria j, assim, infinitamente.

t / logx/x [n]

x ®  ∞

Φ ®  x ®  ®x ®  ∞

      i[n]  [  I= logx/x[n]  ®logk/ k [n ®∞ [n..]

    I = 1

 I= logx/x[n]  ®logk/ k [n ®∞ [n..]

Calculation and geometry graceli prolongamental.

Where each point becomes extensions of straight lines, curves with slopes concave or convex, and in the form of waves flows.

Cálculo e geometria Graceli prolongamental.

Onde cada ponto se transforma em prolongamentos de retas, curvas com inclinações côncava ou convexa, e também em forma de fluxos de ondas.

t / logx/x [n]

x ®  ∞

Φ ®  x ®  ∞

      i[n]  [  ]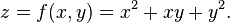

    I = 1

i x= prol lattd.

i z= prol langtd.

i k= prol. altura.

i h= concv.

i j= convex.

i s= Φ

i t= Φ θ

   I = 1

i = prol lattd.

i = prol langtd.

i = prol. altura.

i = concv.

i = convex.

i = Φ

i = Φ θ

i = [a, R, pP, LOGX,X [n]], log r/r [n]]

t / logx/x [n]

x ®  ∞

Φ ®  x ®  ∞

      i  [  z = x² + xy + y²]

    I = 1

i = prol lattd.

i = prol langtd.

i = prol. altura.

i = concv.

i = convex.

i = Φ

i = Φ θ

   I = 1

i = prol lattd.

i = prol langtd.

i = prol. altura.

i = concv.

i = convex.

i = Φ

i = Φ θ

  

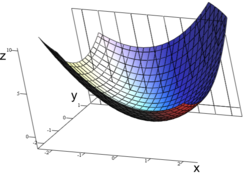
Calculation and geometry graceli prolongamental.

Where each point becomes extensions of straight lines, curves with slopes concave or convex, and in the form of waves flows.

Cálculo e geometria Graceli prolongamental.

Onde cada ponto se transforma em prolongamentos de retas, curvas com inclinações côncava ou convexa, e também em forma de fluxos de ondas.

t / logx/x [n]

x ®  ∞

Φ ®  x ® ∞ 

      i  [  ]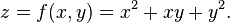

    I = 1

i = prol lattd.

i = prol langtd.

i = prol. altura.

i = concv.

i = convex.

i = Φ

i = Φ θ

   I = 1

i = prol lattd.

i = prol langtd.

i = prol. altura.

i = concv.

i = convex.

i = Φ

i = Φ θ

i = [a, R, pP, LOGX,X [n]], log r/r [n]]

t / logx/x [n]

x ®  ∞

Φ ®  x ® ∞ 

      i  [  z = x² + xy + y²]

    I = 1

i = prol lattd.

i = prol langtd.

i = prol. altura.

i = concv.

i = convex.

i = Φ

i = Φ θ

   I = 1

i = prol lattd.

i = prol langtd.

i = prol. altura.

i = concv.

i = convex.

i = Φ

i = Φ θ

i = [a, R, pP, LOGX,X [n]], log r/r [n]]